Cubic Inches To Gallons Water
Tank Book Calculator
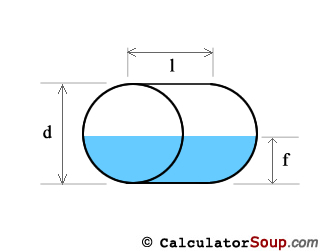
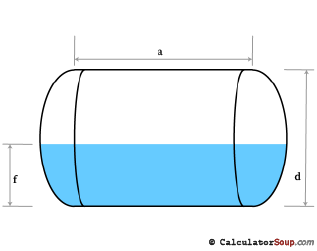
Tank Schematic: Horizontal Cylinder
with flat tank heads
Figurer Use
Guess the total chapters and filled volumes in gallons and liters of tanks such as oil tanks and h2o tanks. Assumes within dimensions of the tank.
Enter U.S. dimensions in feet (ft) or inches (in), or metric dimensions in meters (k) or centimeters (cm). Results are presented in U.S. fluid gallons, Regal (UK) gallons, cubic anxiety (ft³), metric liters and cubic meters (grand³).
*Actual fill volumes may differ. Tank book calculations are based on tank geometries shown beneath. These tank shapes are calculated assuming exact geometric solid shapes such as cylinders, circles and spheres. Actual water and oil tanks may not exist perfect geometric shapes or might accept other features not accounted for here and so, these calculations should only be considered estimates.
Methods to summate the volume of tanks and the volume of a liquid within a tank
The methods below volition give yous cubic measures such equally ft3 or mthree depending on your units of mensurate. If you're calculating filled tank volume by paw using these methods you can covert cubic anxiety to gallons, and cubic meters to liters using our Volume Conversion Calculator.
Horizontal Cylinder Tank

Total volume of a cylinder shaped tank is the area, A, of the circular stop times the length, l. A = πr2 where r is the radius which is equal to 1/2 the bore or d/ii. Therefore:
V(tank) = πr2l
Calculate the filled volume of a horizontal cylinder tank by get-go finding the surface area, A, of a circular segment and multiplying it by the length, l.
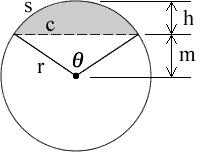
Area of the circular segment, the grayness shaded surface area, is A = (1/2)rtwo(θ - sinθ) where θ = 2*arccos(m/r) and θ is in radians. Therefore, V(segment) = (ane/two)r2(θ - sinθ)50. If the make full pinnacle f is less than ane/2 of d then we use the segment created from the filled height and 5(fill) = 5(segment). However, if the make full height f is greater than 1/2 of d then we use the segment that is created by the empty portion of the tank and subtract it from the full book to get the filled volume; V(fill) = V(tank) - V(segment).
Vertical Cylinder Tank
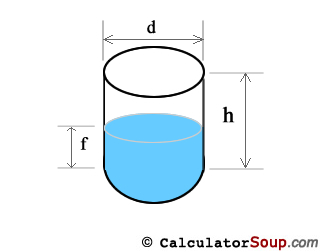
Full book of a cylinder shaped tank is the area, A, of the circular stop times the height, h. A = πr2 where r is the radius which is equal to d/2. Therefore:
V(tank) = πr2h
The filled book of a vertical cylinder tank is but a shorter cylinder with the same radius, r, and diameter, d, but height is now the fill height or f. Therefore:
V(fill) = πr2f
Rectangle Tank
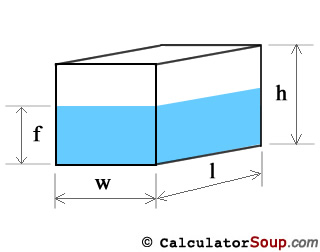
Total volume of a rectangular prism shaped tank is length times width times elevation. Therefore,
V(tank) = lwh
The filled volume of a rectangular tank is but a shorter height with the same length and width. The new height is the fill peak or f. Therefore:
V(fill) = lwf
Horizontal Oval Tank
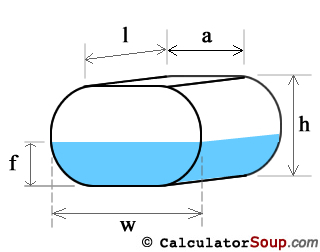
Volume of an oval tank is calculated past finding the area, A, of the end, which is the shape of a stadium, and multiplying it by the length, l. A = πrtwo + 2ra and information technology can be proven that r = h/ii and a = w - h where w>h must ever exist true. Therefore:
V(tank) = (πrii + 2ra)l
Volume of fill of a horizontal oval tank is all-time calculated if nosotros assume it is 2 halves of a cylinder separated by a rectangular tank. We and so calculate fill volume of 1) a Horizontal Cylinder Tank where l = fifty, f = f, and diameter d = h, and 2) a Rectangle Tank where 50 = l, f = f, and rectangle width w is a = due west - h of the oval tank.
V(fill) = V(make full-horizontal-cylinder) + V(fill-rectangle)
Vertical Oval Tank
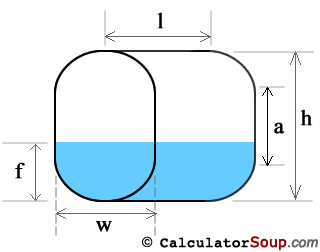
To summate volume of an oval tank find the area, A, of the finish, which is the shape of a stadium, and multiply it by the length, l. A = πr2 + 2ra and information technology tin can be proven that r = due west/2 and a = h - w where h>westward must always be true. Therefore:
Five(tank) = (πr2 + 2ra)l
To calculate fill up book of a vertical oval tank information technology is best if nosotros presume it is 2 halves of a cylinder separated by a rectangular tank. With r = due west/ii = tiptop of the semicircle ends, we can define 3 general fill position areas.
- Fill up, f < r
We calculate fill up volume using the round segment method, as in a Horizontal Cylinder Tank, for the filled portion. - Fill up, f > r and f < (r+a)
The filled volume is exactly one/ii of the cylinder portion plus the volume of fill within the rectangular portion. - Fill, f > (r+a) and f < h
We calculate fill volume using the circular segment method, as in a Horizontal Cylinder Tank, for the empty portion. Volume will be V(tank) - V(segment).
Horizontal Capsule Tank
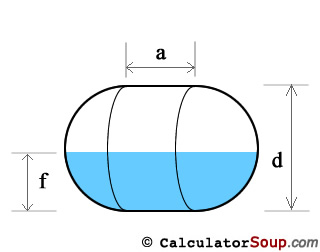
We treat a capsule every bit a sphere of bore d split up in one-half and separated by a cylinder of diameter d and summit a. Where r = d/2.
V(sphere) = (4/three)πr3, and
V(cylinder) = πr2a, therefore
V(capsule) = πr2((four/3)r + a)
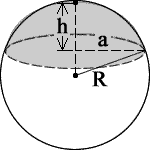
Book of fill for a horizontal capsule is done by using the circular segment method for the Horizontal Cylinder and, with a similar approach, using calculations of a spherical cap for the sphere section of the tank where,
5(spherical cap) = (1/3)πh2(3R - h)
Vertical Capsule Tank
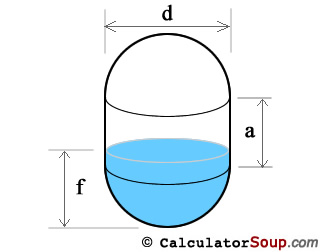
To summate the volume of a vertical capsule tank treat the sheathing every bit a sphere of diameter d split in half and separated by a cylinder of diameter d and height a. Where r = d/2.
V(capsule) = πr2((iv/3)r + a)
To summate fill volume of a vertical capsule calculate in a fashion similar to the method used for the Vertical Oval Tank where r = d/ii = height of each hemisphere terminate.
- Fill, f < r
We calculate fill book using the spherical cap method, for the filled portion. - Fill, f > r and f < (r+a)
The filled book is exactly one/2 of the sphere portion plus the book of fill inside the vertical cylinder portion. - Fill up, f > (r+a) and f < h
We calculate fill volume using the spherical cap method for the empty portion. Volume volition exist V(tank) - 5(spherical cap).
Horizontal ii:1 Elliptical
Horizontal 2:ane Elliptical with 2:1 semi elliptical tank heads
Horizontal Dish Ends
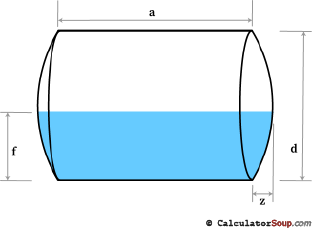
Horizontal Dish Ends with dish only tank heads
Follow CalculatorSoup:
![]()
![]()
Cubic Inches To Gallons Water,
Source: https://www.calculatorsoup.com/calculators/construction/tank.php
Posted by: waxwitte1979.blogspot.com


0 Response to "Cubic Inches To Gallons Water"
Post a Comment